Bab 3 : Fungsi Kuadratik

Assalamualaikum .. 

Apakah fungsi kuadratik? Fungsi itu apa? Haa, kalau nak tahu apa itu fungsi, silakan rujuk tajuk fungsi. Secara umumnya, saya mengklasifikasikan fungsi sebagai hubungan yang berakhlak mulia. Haha. Fungsi hanya ikut satu jalan sahaja. Tujuan dia memang istiqamah. Kalau nak belajar macam mana nak konsisten dalam hidup, kena belajar dengan Abang Fungsi mungkin. Haha.

Ok, lupakan. Teruskan kepada fungsi kuadratik. Bentuk am fungsi kuadratik ialah : 

a, b, dan c merupakan pemalar. x pula merupakan pembolehubah. Kuasa tertinggi bagi persamaan kuadratik ialah 2. Jika kita memplot graf bagi persamaan kuadratik, bentuk yang akan kita peroleh ialah bentuk parabola. Parabola? Hurm, tengok gambar saja. Mesti faham :) 

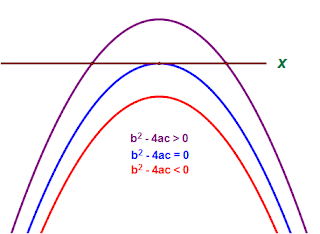
Parabolic Graph

Jika pekali bagi x², iaitu a > 0, maka graf bagi fungsi kuadratik tersebut mempunyai nilai minimum dan bentuknya ialah ∪. 

Jika pekali bagi x², iaitu a < 0, maka graf bagi fungsi kuadratik tersebut mempunyai nilai maksimum dan bentuknya ialah ∩.

Saya sertakan lagi gambar rajah. Gambar juga pandai berkata-kata, letak sahaja, 'mereka' akan 'berbicara' denganmu. Cewah~ 

Keadaan yang mana a > 0

 Keadaan bagi punca f(x) ialah .... Rujuk di sini 

Keadaan yang mana a < 0

Keadaan punca ..

Teruskan kepada soalan ... Soalannya hampir sama dengan subtopik pada bab 2. Mahirkan sahaja diri dengan bab 2, insya-Allah, boleh buat. Saya akan datangkan soalan yang khusus kepada bab ini. 

Soalannya lebih kurang sama kan dengan tajuk 2? Bagus! Mahirkan diri anda! Yakin pada diri bahawa diri boleh buat! Jom teruskan .. 

Tadi, nilai a menentukan sama ada sesuatu graf itu mempunyai titik minimum atau maksimum. Sekarang, kita ingin tentukan koordinat bagi titik minimum atau maksimum tersebut. Untuk mencari titik ini, penting untuk memahirkan diri dengan kaedah penyempurnaan kuasa dua. Rumus asalnya ialah : 

Sekarang, bahagian kanan persamaan akan dipindah kesemuanya ke sebelah kiri. Biarkan sama dengan 0. Rumusnya menjadi : 

Nampak tak perbezaannya? Ingat satu perkara, nilai pekali x², iaitu a wajib sama dengan 1. Cuma beza dengan tajuk 2 ialah tajuk ini perlu difaktorkan bukan dihilangkan terus. Ingat bezanya. Hanya faktor. Nilai a masih wujud, cuma berada di luar kurungan.

Contoh untuk titik minimum, a > 0. 

Faktorkan 2. Letakkan di luar kurungan. Jadi, jawapan telah kita peroleh. Titik minimumnya ialah 31/8. Titik minimum ini mewakili nilai pada paksi-y. Bagi paksi-x pula, untuk menentukannya, hanya ambil nilai yang ada di dalam kurungan. Bagi kes ini, x + 7/4. Jadikannya sama dengan 0. 

x + 7/4 = 0

x = - 7/4

Maka, koordinat titik minimum pada paksi-x ialah -7/4. 

Oleh itu, koordinat titik minimumnya ialah (-7/4, 31/8) 

Contoh untuk a < 0, 

Koordinat titik maksimum pada paksi-y ialah 16/3. Pada paksi-x pula, 

x - 2/3 = 0

x = 2/3

Maka, koordinat titik maksimum ialah (2/3, 16/9)

Titik maksimum/minimum pada paksi-x juga dikenali sebagai titik simetri 'axis of symmetry'. Titik simetri juga boleh dicari dengan menggunakan rumus : 

a = -3, b = 4 

- b/2a = - 4/2(-3)

= 2/3 

Jawapan yang diperoleh sama dengan jawapan di atas.

Langkah-langkah untuk melakar graf : 

1. Tentukan sama ada titik bagi fungsi itu minimum atau maksimum

2. Cari titik itu dengan menyempurnakan kuasa dua.

3. Cari titik persilangan-y. Persilangan-y terjadi apabila x = 0.

4. Cari titik persilangan-x. Persilangan-x terjadi apabila y = 0. Gunakan cara yang sama untuk mencari punca. Sama ada pemfaktoran, penyempurnaan kuasa dua atau rumus.

5. Lakarkan graf.

Graf hanya dilakar, buka diplot. Cuma lakaran. Titik-titik yang diperlukan ialah :

1. Titik maksimum/minimum ---- Ini perkara paling penting

2. Persilangan-y

3. Persilangan-x (Jika ada) 

Saya telah rangkumkan 3 subtopik ke dalam post ini. Subtopik terakhir saya akan postkan berasingan daripada post ini. Semoga dapat buat yang terbaik! Yeah! Anda boleh! Saya boleh!