Assalamualaikum ..
Subtopik ini merupakan subtopik terakhir bagi bab 2 Tingkatan 4. Subtopik ini mengupas tentang keadaan bagi punca bagi satu-satu persamaan kuadratik.
Dalam bab pengenalan, saya telah menulis bahawa, Al-Khwarizmi mengatakan bahawa nilai pembezalayan mestilah positif. Tapi, itu dulu. Dan sekarang telah berubah. Tapi, sayangnya, tajuk itu tidak termasuk dalam sukatan. Kalau ingin tahu, sila tanya Pak Cik Google, taip sahaja nombor khayalan atau dalam bahasa Inggerisnya ialah imaginary numbers.
Ok, berbalik kepada tajuk asal. b2 − 4ac dinamakan pembezalayan atau discriminant bagi mana-mana persamaan kuadratik. Terdapat 3 keadaan bagi pembezalayan ini. Jom kita layan~
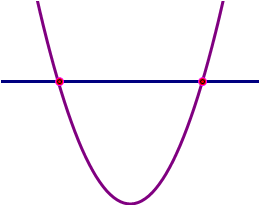
1. Keadaan yang mana nilai pembezalayan lebih besar daripada 0. Punca bagi persamaan kuadratik ini ada 2, dan kedua-duanya berbeza. Puncanya juga nyata.
2. Keadaan yang mana nilai pembezalayan sama dengan 0. Kedua-dua punca bagi persamaan ini sama. Puncanya nyata. DIkenali juga sebagai tangen kerana hanya bersilang pada satu titik sahaja.
3. Keadaan yang mana nilai pembezalayan lebih kecil daripada 0. Puncanya tidak nyata atau lebih dikenali imaginary.
Gambar rajah di atas merupakan keadaan bagi punca-punca bagi persamaan kuadratik.
Teruskan kepada contoh, perbanyakkan contoh baru cepat faham. Matematik ni memang mudah, jangan kata susah. Kalau rajin buat latihan, tanya orang, gali selidik, insya-Allah, dapat skor.
Saya datangkan 3 contoh. Setiap contoh mewakili bagi setiap gambar rajah. Ingat rumus pembezalayan. Kalau dalam dewan tak ingat, jangan risau! Superman ada! Haha. Tak, bukan Superman, tapi rumus telahpun disediakan di hadapan kertas. Hanya ambil rumus yang ada di dalam punca kuasa. Ingat kembali rumus untuk mencari punca.
Pastikan simbol positif dan negatif diambil kira. Ini penting! Jika tersalah ambil, jawapan anda akan salah. Untuk memudahkan anda, catatkan dahulu nilai bagi a, b dan c. Mudah-mudahan, tidak tersalah ambil nilai.
Ok, contoh soalan seterusnya. Soalan seterusnya lebih realistik. Haha.
Selepas baca soalan, perkara pertama yang perlu lihat ialah kata kunci soalan. Kata kunci pada soalan ini ialah dua punca berbeza. Maka, apabila dua punca berbeza, b2 − 4ac > 0.
Oh, jangan lupa juga untuk susun dalam bentuk am. Kenali yang mana nilai bagi a, b dan c. Ketiga-tiga nilai ini dapat dikenali dengan anu x selepasnya. Jika x kuasa dua, maka pekalinya ialah a. Jika x sahaja, maka pekalinya ialah b. Jika tiada x, maka pekalinya ialah c. Pekali juga dikenali sebagai coefficient.
Satu lagi contoh. Mungkin masih dalam keadaan blur bagi yang mula belajar.
Satu lagi contoh. Mungkin masih dalam keadaan blur bagi yang mula belajar.
Soalan ini agak mencabar, mungkin dalam 3 atau 4 markah. Pastikan susun dalam bentuk am dahulu.
Bagi nilai b dalam soalan ini, perlu difaktorkan dahulu. Ini penting untuk memperoleh nilai sebenar bagi b. Ingat! Anu x tidak perlu diambil dalam pembezalayan. Hanya ambil nilai pekali sahaja. Nilai pekali sahaja.
Kembangkan dengan hati-hati, ambil kira nilai positif/negatif. Gunakan ilmu yang telah dipelajari semasa tingkatan 3 bab 6 Algebraic Expressions III.
Kembangkan dengan hati-hati, ambil kira nilai positif/negatif. Gunakan ilmu yang telah dipelajari semasa tingkatan 3 bab 6 Algebraic Expressions III.
Semua topik telahpun siap dikupas. Seterusnya, saya akan pergi kepada bab 3 : Fungsi Kuadratik. Kita akan mengenal ciri-ciri persamaan kuadratik pada satah Cartesan. Ada soalan, sila tanya. Jangan malu.
Good Luck!












saya nak tanya soalan ni : jika salah satu punca bagi persamaan 2xkuasa dua + px +9 = 0 adalah dua kali ganda punca yang satu lagi, cari nilai yang mungkin bagi p.. tolong saya >.< sbb kali ni, die xtnye persamaan tpi nk nilai unknown to sndiri
ReplyDeletetolonggg saya.. soalan clone spm 2009.
ReplyDeletediberi -3 ialaah satu drpd punca persamaan kuadratik xkuasa dua + x - m = 0 . cari nilai m .
Saya nak tanya kalau fungsi cekung ke bawah adakah berbentuk masam iaitu fungsi kuadratik maksimum?? Pls help
ReplyDeleteSaya nak tanya kalau fungsi cekung ke bawah adakah berbentuk masam iaitu fungsi kuadratik maksimum?? Pls help
ReplyDeleteYep
Deletetolong saya!
ReplyDeleteSalah satu punca persamaan kuadratik 2xkuasa dua +px+16=0 adalah dua kali punca yang satu lagi.